Exploring the fmp12 file format; or: what was my password again?

136 minute read

Introduction

I had been planning for a while to dive deeper into the fmp12 file format to explore how data is organized and how accounts and passwords are stored. A few months ago, I finally found the time to do it.

The first thing I noticed was just how little information publicly exists about the file format and especially about account and password storage.

The only information on the latter was that “a one-way hash” is used for storing passwords and that there are some password reset tools that – according to forums – might work but would also “damage” your file, without any further clarification.

In my opinion this kind of knowledge shouldn’t only exist for password recovery tool vendors. If you invest a lot time and money into your fmp12 solution, you should know how much or how little local accounts/passwords protect distributed files and also what the reset tools actually do to your files.

It should come to no surprise to some people that you can get around the password protection of unencrypted local files. However, I’ve also spoken to many people in the past who thought a password protected (local) fmp12 file is literally protected if you don’t have the password (i.e. you cannot get into the file to access the data or code).

In June 2024, I gave a talk about this topic at the dotfmp conference. This post will follow the general flow of the presentation. Just like in the talk, we start at the very beginning with some basics (I have also included the number base conversions to keep it complete).

The following article does not come with a proof-of-concept code to reset account passwords for fmp12 files, but it will give you an understanding of the protections in place.

A disclaimer up front: all information presented in the following is based on my observations and some assumptions. As there is no open specification of the file format, we just have to accept that certain things cannot be fully confirmed.

Also note that this is not a post about a vulnerability but rather an exploration into how things works internally in an fmp12 file. We are not talking about accessing a remote file on FileMaker Server.

TL;DR: If you have access to a local fmp12 file, account passwords can be reset. If you just want to read some data from a file, you obviously don’t even need an account/password. If you want to properly protect your local files, use the encryption at rest feature – it’s designed for exactly this.

Number bases / radices, bits and bytes

Over the course of this blog post we are going to look at a lot of raw byte values. Some values are better represented in binary or hexadecimal form.

So let’s start with a quick refresher on how to read numbers in base 10, base 2 and base 16. If you deal with binary and hex values all the time, feel free to skip this section.

Base 10

In everyday life we’re mostly using the base 10 numeral system. If you see the number 2024, you don’t think much about it because you’re used to working with decimal numbers.

But let’s have a look at the formula that actually lets you compute the value from the individual digits of a decimal number:

d3 d2 d1 d0
|  |  |  |
|  |  |  +-- The ones
|  |  +-- The tens
|  +-- The hundreds
+-- The thousands

In base 10 every digit can represent one of 10 values (0-9) and each of the digits contributes to the total value.

The number 2024 can be represented like so:

2  0  2  4
|  |  |  |
|  |  |  +-- The ones
|  |  +-- The tens
|  +-- The hundreds
+-- The thousands

So to get to two-thousand-twenty-four, we can just read what every place contributes and add these values together:

\[d_{N-1} \times 10^{N-1} + d_{N-2} \times 10^{N-2} + d_{N-3} \times 10^{N-3} + d_{N-4} \times 10^{N-4}\] \[d_{3} \times 10^3 + d_{2} \times 10^2 + d_{1} \times 10^1 + d_{0} \times 10^0\] \[2 \times 10^3 + 0 \times 10^2 + 2 \times 10^1 + 4 \times 10^0\] \[2 \times 1000 + 0 \times 100 + 2 \times 10 + 4 \times 1\] \[2000 + 0 + 20 + 4\] \[2024\]

As you will see in the following, the same formula also applies to other bases if the base value is swapped out accordingly.

Base 2

In base 2 every digit can have one of two values, 0 or 1. Taking a sample value of 0b1101 (decimal 13), we can compute the decimal value using the same steps as before:

d3 d2 d1 d0
|  |  |  |
|  |  |  +-- The ones
|  |  +-- The twos
|  +-- The fours
+-- The eights


1  1  0  1 = decimal 13
|  |  |  |
|  |  |  +-- The ones
|  |  +-- The twos
|  +-- The fours
+-- The eights

\[d_{N-1} \times 2^{N-1} + d_{N-2} \times 2^{N-2} + d_{N-3} \times 2^{N-3} + d_{N-4} \times 2^{N-4}\] \[d_{3} \times 2^3 + d_{2} \times 2^2 + d_{1} \times 2^1 + d_{0} \times 2^0\] \[1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0\] \[1 \times 8 + 1 \times 4 + 0 \times 2 + 1 \times 1\] \[8 + 4 + 0 + 1\] \[13\]

Often times the prefix 0b is used to indicate that you’re looking at a binary number.

Base 16

Lastly, we have base 16, which will be the most used in the contents to follow. In base 16 we have 16 possible values for every digit, 0 to 15. The values from 10 to 15 are represented by letters a to f.

Hexadecimal values are usually prefixed with 0x.

To get the decimal value from a hexadecimal number, we can follow the same steps as before, but use 16 as the base:

d3 d2 d1 d0
|  |  |  |
|  |  |  +-- The ones
|  |  +-- The 16s
|  +-- The 256s
+-- The 4096s


C  A  F  E = 51966
|  |  |  |
|  |  |  +-- The ones
|  |  +-- The 16s
|  +-- The 256s
+-- The 4096s

\[d_{N-1} \times 16^{N-1} + d_{N-2} \times 16^{N-2} + d_{N-3} \times 16^{N-3} + d_{N-4} \times 16^{N-4}\] \[d_{3} \times 16^3 + d_{2} \times 16^2 + d_{1} \times 16^1 + d_{0} \times 16^0\] \[12 \times 16^3 + 10 \times 16^2 + 15 \times 16^1 + 14 \times 16^0\] \[12 \times 4096 + 10 \times 256 + 15 \times 16 + 14 \times 1\] \[49152 + 2560 + 240 + 14\] \[51966\]

Bits and Bytes

As the last theoretical bit (pun not intended :-)), let’s have a look what is in a byte and how we can represent bytes in a clear way:

1 byte = 8 bits = 256 possible values (0 to 255)

Example: 0b10000001 = 0x81 = 129

When dealing with 16, 32, or 64-bit values it quickly becomes impractical to use a base 2 or base 10 representation of values.

Looking at just a 16-bit (2-byte) value, you can tell that 16 0s and 1s are hard to make sense of (unless they are all the same). And in a decimal representation it’s hard to know how many bytes a number represents.

But seeing the same value represented in hexadecimal, we can immediately spot that it’s two bytes (1 byte can be represented in two hex digits):

0b1111111111111111 = 0xffff = 65535
16 bits            = 2 bytes

The fmp12 file format

Visual inspection and header

Now that we’ve covered the theoretical background, let’s see how an fmp12 file actually looks like when examining the raw bytes of it:

          |----------- magic bytes -----------|--
00000000: 0001 0000 0002 0001 0005 0002 0002 c048  ...............H
          format--|
00000010: 4241 4d37 0000 1000 0000 0000 0000 0000  BAM7............
00000020: 0000 0000 0000 0000 0000 0000 0000 0000  ................
00000030: 0000 0000 0000 0000 0000 0000 0000 0000  ................
00000040: 0000 0000 0000 0000 0000 0000 0000 0000  ................
00000050: 0000 0000 0000 0000 0000 0000 0000 0000  ................
00000060: 0000 0000 0000 0000 0000 0000 0000 0000  ................
00000070: 0000 0000 0000 0000 0000 0000 0000 0000  ................
00000080: 0000 0000 0000 0000 0000 0000 0000 0000  ................
00000090: 0000 0000 0000 0000 0000 0000 0000 0000  ................
000000a0: 0000 0000 0000 0000 0000 0000 0000 0000  ................
...

As is common for many formats, the file begins with a magic byte-sequence signature. This is followed by what appears to be the internal name of the format: HBAM7.

If we were to look at an encrypted file the format would say HBAMe and the rest of the file would by, well, encrypted.

A quick glance at the file also reveals its organization into 4-kilobyte blocks. Before each multiple of 4096 bytes we see a bunch of null bytes (0x00) as the blocks are usually not completely filled.

Helpful resources

As noted earlier, there are very few online resources about fmp12. However, the following three were valuable for kickstarting the process of understanding the file format:

The first two are DevCon talks which give a few insights about how FileMaker Pro/Server logically organizes files. The third, fmptools, is a repository containing C code to parse and extract table data from fmp12 (and older) files and does a great job documenting many of the byte-codes used in the payloads of the 4K blocks.

If you want to get familiar with the format I highly recommend starting by writing a parser yourself and implementing the codes documented in this repository.

Block structure

The 4096 byte blocks in the file are organized as a doubly linked list, meaning each block knows the ID of the previous and next block.

This information (and other meta data, e.g. if a block was deleted or not) is stored in the first few bytes of every block.

So by parsing the block header, we can determine the offset to which we need to jump next in the file.

                    |prev ID| |next ID|
00001000: 0000 0000 0000 0000 0000 0043 0001 0de7  ...........C....
                    |- beginning of payload ----
00001010: 0000 0894 1b00 0100 0000 0220 0220 8703  ........... . ..
          -- cont. until end of block---------...
00001020: 0300 0000 41c3 0600 0000 4220 88c3 0100  ....A.....B ....

Payload

The payload in each block consists of a sequence of bytes, beginning with a code that describes the following data chunk or the operation to be performed.

The op-codes 0x40 (POP) and 0x20 (PUSH) are used for constructing path information, such that the application reading the file is able to address the individual pieces of data later on.

The data chunks we are interested in for the purpose of figuring out the account and password storage are mostly the key-value pairs (examples to follow). Be aware, though, that we have to have knowledge about all byte-codes in a payload of a block to be able to parse that block in its entirety.

Examining a number of sample files yourself, you will likely notice that there are more than just the byte-codes documented in the fmptools repository.

When encountering a new/unknown code, there are two options: you could either try to reverse-engineer it or skip processing the rest of the payload and move on to the next block. For the purpose of learning about accounts and passwords it’s generally OK to skip ahead as long as the unknown codes don’t appear in the same block as the information we are interested in.

Encoding of data, and payload examples

When you start exploring a file format and have an application at hand that can write data in that format, one of the easiest experiments you can do is to let the application write a known string into the file and see how that string is represented.

Let’s say we were to open an fmp12 file and chose the name AAAAAA for a field, a script, an account name or anything else. Observing how the file changes once that name is committed would give us a clue on a) where the data is stored in the file, and b) how the data is stored.

If you perform this experiment, you will quickly notice that the plaintext AAAAAA does not appear anywhere in the file. Instead, each byte you enter is stored in a transformed (but predictable) manner. The six As do not appear as six instances of 0x41 (decimal 65, the ASCII code for capital A) but rather as 0x1b.

Why 0x1b? It turns out that all the data in fmp12 files is XORed with the byte 0x5a – I assume just for a little obfuscation.

How would you find the XOR byte? You just try out all possible byte values and see which one gives you back 0x41 (A) again.

Let’s have look at a short example of the bitwise XOR operation in case you are not familiar with it.

XOR example

We established that 0x1b ^ 0x5a = 0x41 = 65 = A (the caret denoting the XOR operator).

XOR stands for “exclusive or” and the result of the operation is only true (1), if the two given inputs differ.

And since we are performing a bit-wise operation, our inputs to XOR are the individual bits of the bytes.

Sticking with the example from above, this looks like follows:

0b00011011 ^ 0b01011010 = 0b01000001

00011011 <== 0x1b
01011010 <== 0x5a
--------
01000001 <== 0x41

Going back to the formula from the very beginning, we can see that \(2^6 + 2^0 = 65\), and 65 is again the ASCII code for “A”.

Key-value example

Let’s now look at an example of a data chunk inside a payload.

0x06 0x10 0x05 0x1b 0x3e 0x37 0x33 0x34

In this case 0x06 would be the code for a key-value pair.

0x10 would be the key, and 0x05 the length of the data for this key.

Looking at the next 5 bytes (length), we have 0x1b 0x3e 0x37 0x33 0x34.

Performing an XOR operation with each byte and the constant 0x5a as explained above, we get:

0x1B ^ 0x5A = 0x41, 0x3E ^ 0x5A = 0x64, ..., 0x34 ^ 0x5A = 0x6E
0x41 = ASCII "A", 0x64 = "d", ... 0x6E = "n"
"Admin"

So the example above would store the string Admin with key 0x10.

Path operation example

As mentioned before, the payload also contains op-codes for PUSH and POP operations. Let’s look at an example and assume the current path is 17.1 (arbitrary for this example):

0x40 0x40 0x20 0x17 0x80 0x20 0x01 0x80 0x20 0x01

We start by looking at the first byte, determine it’s a POP operation and thus pop off the 1 of our example path, leaving only 17.

Another POP operation (second byte) also pops off the 17, leaving us with an empty path.

The third byte is the op-code for a PUSH operation with the value 0x17. So we push 0x17, or 23 in decimal, onto the path (not to be confused with the decimal 17 in the beginning).

The fourth byte is a NOP, a no-operation instruction. Thus, nothing changes.

Then, we continue with another PUSH of the value 1, meaning our path becomes 23.1.

We continue in the same way as before and eventually arrive at a path of 23.1.1. Here is a list of the instructions in less verbose form:

0x40: POP one off path -> 17
0x40: POP one off path -> empty
0x20 0x17: PUSH 0x17 -> 23
0x80: NOP -> 23
0x20 0x01: PUSH 0x01 -> 23.1
0x80: NOP -> 23.1
0x20 0x01: PUSH 0x01 -> 23.1.1

If the key-value pair from the previous example would follow, it would have the path 23.1.1.16 (16, or 0x10, being the key).

How do we get to the accounts?

With the information given so far we are able to write a simpler parser for any fmp12 file (assuming we have knowledge of all byte-codes used in the file).

How does this help us learn more about the stored accounts and passwords? We can open a few sample files and check where account names, such as Admin, are stored, then note down their path (we know the account names to search for as we are parsing our own files).

What we find is that account information is generally stored at path 23.1.5.N, where N is the account number. So the first account would be in 23.1.5.1, the second account in 23.1.5.2, and so on. The parent path 23.1.5 always stays the same.

Note that you don’t need any account/password if all you want is to read some data from a file. But we want to find out how much accounts protect a local file from being accessed the “normal” way and if passwords can easily be reset.

Where exactly is the name stored and what else is “nearby”? Let’s have a look at a chunk of a payload:

[...]

00008190: 020e fc03 0908 9fa1 5b80 0596 6aa0 4020  ........[...j.@
000081a0: 0280 0604 1005 407c dc76 b7f1 fd29 ac5a  ......@|.v...).Z
000081b0: 9c79 1af6 b806 063b 0104 72b2 e83c 04a8  .y.....;..r..<..
000081c0: bd2b fe3c bc1f 3d1f 0b69 df8e 93c6 542e  .+.<..=..i....T.
000081d0: 4786 01b0 5d26 1d38 cead d523 0fc1 62a5  G...]&.8...#..b.
000081e0: 6dfa e831 7a99 0ad9 82a8 8efe 9a83 92a5  m..1z...........
000081f0: 0e71 3f06 0a09 089f a15b 8005 9674 3002  .q?......[...t0.
00008200: 0b01 0106 1005 1b3e 3733 3420 5d80 2800  .......>734 ].(.
00008210: 0080 2011 8020 1880 4040 4040 06d8 1071  .. .. ..@@@@...q

[...]

Let’s add some color to better identify the byte-codes (red), the arguments/keys/lengths (green) and the actual data (blue). The account name “Admin” (XORed) is highlighted in blue.

Account information in payload

Parsing this payload would look something like this:

(Current path 23.1.5.1)

0x40 (POP)
0x20 (PUSH) 0x2
Path is now 23.1.5.2

0x06 (Key Value) with key 0x04 and length 0x10 (16 bytes)
Path 23.1.5.2.4 ==> 05407cdc76b7f1fd29ac5a9c791af6b8

0x06 (Key Value) with key 0x06 and length 0x3b (59 bytes)
Path 23.1.5.2.6 ==> 010472b2e83c04a8bd2bfe3cbc...e9a8392a50e713f

0x06 (Key Value) with key 0x0a and length 0x09 (9 bytes)
Path 23.1.5.2.10 ==> 089fa15b8005967430

0x02 (Key Value) with key 0x0b and a length of 2 bytes
Path 23.1.5.2.11 ==> 0101

0x06 (Key Value) with key 0x10 and length 0x05 (5 bytes)
Path 23.1.5.2.16 ==> 1b3e373334 ===> ("Admin" XORed with 0x5a)

By looking at the values while performing account changes (for example via FileMaker Pro) we can draw some conclusions and make assumptions.

The account name is always stored with key 16 or 0x10, and XORed with 0x5a (just like the other data).

The value at key 0x04 (05407cdc76b7f1fd29ac5a9c791af6b8) has a fixed length of 16 bytes and the value completely changes when changing an account password (or other account information for that matter). Given the length of 16 bytes and its behavior, we can make the assumption that this could potentially be an MD5 hash.

The 59-byte long value at key 0x06 (010472b2e83c04a8bd2bfe3cbc...e9a8392a50e713f) also changes when we change an account password. Two things stand out here, though: the length always changes (even for the same password), and the first byte is always 0x01.

Hint: for the rest of this blog post we will mostly talk about these two values (key 0x04 and 0x06).

What to do with this information?

To make further progress, we have three options:

Continue to make slight changes to the file via FileMaker Pro, and observe how these changes are represented in the file
Open the file with any kind of application designed to read fmp12 files (e.g. FileMaker Pro, Server, FMMigrationTool, …), attach a debugger and read some assembly code
Just YOLO it, start changing some bytes in the file and see what happens 🤞

As professionals, we obviously choose option 3 ;-)

So what happens when we, for example, just change the account name at path 23.1.5.2.16?

Can we still open the file?

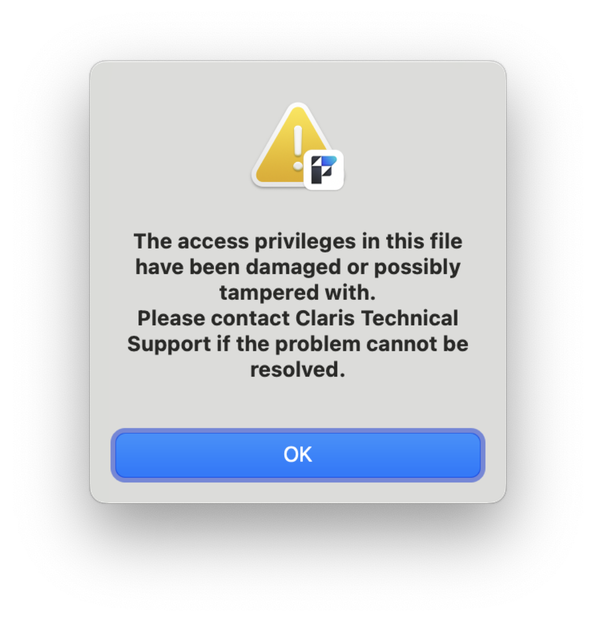
Tamper alert

I guess that’s what you get when you change stuff without really knowing what’s up :-)

Lessons learned so far

We might not have succeeded yet, but the failures and observations gave us new insight:

If we modify an account name, we get a tamper alert
If we modify any of the potential hashes nearby, we get a tamper alert
If we modify a buch of other stuff in the file, we get a tamper alert
Given the above points, we can assume that there’s likely a checksum of all the account information
We learned that accounts generally have the same parent path 23.1.5
We learned that the 16-byte value at key 0x04 has a fixed length and changes when the password is changed
We learned that the 59-byte value at key 0x06 has a variable length and changes when the password is changed (with the exception of the first byte, which is always 0x01)

Time for some debugging

It seems, to make progress, we have to see what is actually going on (what algorithm is used? is there a salt value? …) in a program that can read fmp12 files.

As explained in last year’s post about deciphering the FileMaker keystore, the easiest way to find a starting point of where to look inside the program is to dump the symbol table and then set breakpoints at interesting locations of the program.

We will use gdb as the debugger and the FMDataMigration tool as the target. Being able to pass an account name and password directly on the command line is more convenient than debugging a UI application (FileMaker Pro).

As target for the migration tool we choose any sample file of which we know the account and password. Launching the debugger could look like this:

gdb --args FMDataMigration -src_path /path/to/source/test.fmp12 -src_account Admin -src_pwd whatever -clone_path /path/to/clone/test\ Clone.fmp12 -clone_account Admin -clone_pwd whatever -target_path /path/to/migrated/test.fmp12 -force

Note that we pass Admin as account name, and whatever as password.

Figuring out the password hash

Looking at the known function names (dumping symbols), we can note down everything that could be related to password hashing/reading/writing, then set breakpoints at these locations.

One very obvious function to start with is Draco::PasswordHash::ComputePasswordHash.

We can set a breakpoint, then (for every call) look up the arguments passed to the function and then see if we can make sense of any of them (for example, if the values also show up in the fmp12 file).

I debugged the application on a Linux machine on x86_64, so based on the calling conventions the first arguments are generally passed in registers rdi, rsi, rdx, rcx, r8 and r9.

Values passed to ComputePasswordHash

Once a breakpoint has been triggered, we can look at the register values:

(gdb) info reg

rcx            0x7ffff75529e0 # static known string (starts with "File" :-))

rdx            0xa            # length of value of address pointed to by rsi (10 bytes)

rsi            0x7fffffffa0d9 # points to value we saw at path 23.1.5.2.6
                              # 01===>0472b2e83c04a8bd2bfe<===3cbc1f..8efe9a8392a50e713f

rdi            0x7fffffffb2c0 # points to pointer where given password is stored
                              # (char16, 2-byte chars)

r8             0x1e           # length of value in rcx (30 bytes)

r9             0x1            # value of 1

+ some values on the stack

As commented above, we see several interesting values. rdi points to the password we passed in as command line argument (as 16-bit characters). rsi points to a part of the 59-byte value previously seen in the file at path 23.1.5.2.6. Assuming the next argument (rdx) is the length, we can read 10 bytes from rsi and get 0472b2e83c04a8bd2bfe.

rcx points to a constant string which starts with File (hint, hint), but has a length of 30 bytes (r8).

r9 contains 0x01 which may or may not be relevant to what we are trying to find out. We note it down in any case.

What do we know so far?

While not certain, we can make an assumption that the first 10 bytes after the 0x01 is the salt value (as storing it next to a password hash would make sense). To clarify, looking at the 59-byte byte-sequence from above, the 10-bytes are these:

01 --> 0472b2e83c04a8bd2bfe <-- 3cbc1f3d1f0b69df8e93c6542e478601b05d261d38ceadd5230fc162a56dfae8317a990ad982a88efe9a8392a50e713f

We have discovered a 30-byte constant value that seems to be somehow incorporated into the password hash computation (an assumption made based on the passed values).

We have also discovered a constant value of 0x01 which might be relevant to the hash.

And we have found out that the clear password which we pass on the command line ends up being passed to the ComputePasswordHash function as well.

Digging deeper

We know the input to the function. But what exactly happens within it?

To figure this out let’s have a closer look at one of the loops in that function:

[...]
0x00007ffff4c328f4 <+132>:   div    %r13d
0x00007ffff4c328f7 <+135>:   movzbl (%r14,%rdx,1),%ebx
0x00007ffff4c328fc <+140>:   shl    $0x8,%ebx
0x00007ffff4c328ff <+143>:   lea    0x1(%rcx),%eax
0x00007ffff4c32902 <+146>:   xor    %edx,%edx
0x00007ffff4c32904 <+148>:   div    %r13d
0x00007ffff4c32907 <+151>:   movzbl (%r14,%rdx,1),%eax
0x00007ffff4c3290c <+156>:   or     %ebx,%eax
 ===> 0x00007ffff4c3290e <+158>:   xor    (%rdi,%rbp,2),%ax <===
0x00007ffff4c32912 <+162>:   rol    $0x8,%ax
0x00007ffff4c32916 <+166>:   mov    %ax,(%rdi,%rbp,2)
0x00007ffff4c3291a <+170>:   add    $0x2,%ecx
0x00007ffff4c3291d <+173>:   mov    %esi,%ebp
0x00007ffff4c3291f <+175>:   add    $0x1,%esi
0x00007ffff4c32922 <+178>:   cmp    %rbp,%r9
0x00007ffff4c32925 <+181>:   ja     0x7ffff4c328f0
[...]

Looking at the assembly code, we can identify an XOR operation (shown with arrows above) with two 16-bit values. Calculating both the effective memory address and looking up the value in ax (lower 16 bits of rax), we can see that in the first iteration the values are 0x77 0x00 (little endian) and 0x46 0x69, respectively.

Looking up the ASCII character for 0x0077, we can identify it as w – the first character (zero-extended to 16-bits) of our whatever password.

Doing the same for 0x46 and 0x69, we arrive at Fi, the first two characters (1 byte each, so also 2 bytes/16-bits) of the constant string we saw earlier.

The result of the XOR operation is thus 0x0077 ^ 0x4669 = 0x461e.

Continuing for the whole length of the password, we arrive at a new sequence of bytes that we note down for later.

Looking at additional calls

Inspecting the function further we see two interesting calls:

 ===> 0x00007ffff4c3294e <+222>:   callq  0x7ffff4c08b30 <EVP_sha1@plt> <===
0x00007ffff4c32953 <+227>:   mov    0x70(%rsp),%rbp
0x00007ffff4c32958 <+232>:   mov    0x10(%rsp),%rdi
0x00007ffff4c3295d <+237>:   mov    0x18(%rsp),%esi
0x00007ffff4c32961 <+241>:   add    %esi,%esi
0x00007ffff4c32963 <+243>:   mov    0x8(%rbp),%ebx
0x00007ffff4c32966 <+246>:   mov    %r12,%rdx
0x00007ffff4c32969 <+249>:   mov    %r15d,%ecx
0x00007ffff4c3296c <+252>:   mov    0xc(%rsp),%r8d
0x00007ffff4c32971 <+257>:   mov    %rax,%r9
0x00007ffff4c32974 <+260>:   pushq  0x0(%rbp)
0x00007ffff4c32977 <+263>:   push   %rbx
 ===> 0x00007ffff4c32978 <+264>:   callq  0x7ffff4c087e0 <PKCS5_PBKDF2_HMAC@plt> <===
0x00007ffff4c3297d <+269>:   add    $0x10,%rsp
0x00007ffff4c32981 <+273>:   mov    0x10(%rsp),%rdi
0x00007ffff4c32986 <+278>:   lea    0x20(%rsp),%rax
0x00007ffff4c3298b <+283>:   cmp    %rax,%rdi

The two highlighted functions are from the OpenSSL library.

Since the library is open source, we can look up code and documentation and know for sure what arguments are expected to be passed to these functions.

So just like before, we can set a breakpoint at the key derivation function PBKDF2 (explained in more detail in my other post) and look at the registers again to see what values are being passed.

This is the function signature:

int PKCS5_PBKDF2_HMAC(const char *pass, int passlen,
                      const unsigned char *salt, int saltlen, int iter,
                      const EVP_MD *digest,
                      int keylen, unsigned char *out);

And these are the register values when calling the function:

(gdb) info reg
rax    0x7ffff34b47e0      140737275185120
rbx    0x14                20
rcx    0xa                 # length of salt (10 bytes)
rdx    0x7fffffffa0d9      # points to 10 byte (rcx) salt (now confirmed) 0x04 0x72 ... (x/10xb $rdx)
rsi    0x10                # length of xored password (16 bytes)
rdi    0x60a38220          # points to 16 (rsi) bytes of XORed password 0x46 0x1e ... (x/16xb $rdi)
rbp    0x7fffffffa350      0x7fffffffa350
rsp    0x7fffffffa038      0x7fffffffa038
r8     0x1                 # the value of 1 seen before, the iteration count
r9     0x7ffff34b47e0      # points to SHA1 context

On stack: keylen of 20 and address for out

I commented each relevant register value above. To summarize it again:

We pass in our XORed password (rdi) from above. The value for the salt argument (rdx) is the 10 bytes we identified earlier (so it’s now confirmed that it indeed is a salt value), an iteration count (r8) of 1 (the 0x01 value we saw earlier), and a pointer to the SHA1 hashing function (r9) (we saw it being initialized above). Additionally, a desired key length of 20 and an address for the output is passed.

Letting this function run and observing the result written to *out we can see that it is exactly the 20 bytes after the previously identified salt value in the 59-byte long sequence of bytes at path 23.1.5.2.6.

Summary so far

Of the value at 23.1.5.2.6 we now know the following components:

010472b2e83c04a8bd2bfe3cbc1f3d1f0b69df8e93c6542e478601b05d261d38ceadd5230fc162a56dfae8317a990ad982a88efe9a8392a50e713f
| |                   |                                       |
| |                   |                                       +--> Still unknwon
| |                   +--> The 20-byte derived key / password hash
| +--> The 10-byte salt value
+--> Always 1; we could assume that this is some sort of version number, in case the algorithm changes in the future

To arrive at this result, we saw that we have to have the password (char16), a salt and a fixed value.

In a loop, we XOR the password with the fixed value.

We then feed the XOR result into PBKDF2 with a SHA1 digest function.

And out comes the hash that is being stored in the fmp12 file.

Figuring out the variable-length “checksum”

So what is the still unknown part of this 59-byte sequence? And why does it change in length every time we change a password?

To figure this out, we have dig into another function called Draco::DBPassword::Read:

[...]
0x00007ffff5e61aeb <+459>:   mov    $0x1,%edx
0x00007ffff5e61af0 <+464>:   movzbl 0x1a(%rsp,%rdx,1),%ebx
 ===> 0x00007ffff5e61af5 <+469>:   xor    0x10(%rsp,%rdx,1),%bl <===
0x00007ffff5e61af9 <+473>:   movzbl 0x2e(%rsp,%rdx,1),%ecx
0x00007ffff5e61afe <+478>:   cmp    %bl,%cl
0x00007ffff5e61b00 <+480>:   sete   %al
0x00007ffff5e61b03 <+483>:   cmp    %rsi,%rdx
0x00007ffff5e61b06 <+486>:   jae    0x7ffff5e61b14
0x00007ffff5e61b08 <+488>:   add    $0x1,%rdx
 ===> 0x00007ffff5e61b0c <+492>:   cmp    %bl,%cl <===
0x00007ffff5e61b0e <+494>:   je     0x7ffff5e61af0
0x00007ffff5e61b10 <+496>:   jmp    0x7ffff5e61b14
0x00007ffff5e61b12 <+498>:   and    %cl,%al
0x00007ffff5e61b14 <+500>:   test   %al,%al
[...]

Here, we see again a XOR operation in a loop. And if we look at the values in memory and the register for each iteration, we will find that each byte of the password hash is XORed with each byte of the salt value.

Looking at the result, we see that it matches the previously unknown remainder of the 59-byte sequence mentioned earlier.

We also see that every computed byte (XOR result) is compared to the stored byte – so any variation between stored and computed will likely trigger the tamper alert.

Visualizing the first few operations of this loop:

010472b2e83c04a8bd2bfe3cbc1f3d1f0b69df8e93c6542e478601b05d261d38ceadd5230fc162a56dfae8317a990ad982a88efe9a8392a50e713f
  | | |               | | |                                   ^ ^ ^
  | | |               | | |                                   | | |
  | | |               | | |                                   | | |
  | | |               | | |                                   | | |
  | | |               v | |                                   | | |
  +-|-|---> xor(0x04, 0x3c) = 0x38 ---------------------------+ | |
    | |                 | |                                     | |
    | |                 v |                                     | |
    +-|-----> xor(0x72, 0xbc) = 0xce ---------------------------+ |
      |                   |                                       |
      |                   v                                       |
      +-------> xor(0xb2, 0x1f) = 0xad ---------------------------+

You might be wondering how you can XOR salt and password if they differ in length. What actually happens is XOR(salt + password, password), with the password being extended by the XOR result as the loop progresses.

Why variable length?

What we don’t yet understand is why the XOR byte-sequence has a variable length, i.e. is often truncated.

The answer is to be found in yet another function: Draco::DBUserAccount::MatchPasswordData.

Setting a breakpoint, running the program and taking a closer look, we can see the following instructions:

0x00007ffff5e63901 <+225>:   movzbl 0x28c(%rsp),%esi
0x00007ffff5e63909 <+233>:   and    $0x1f,%esi

By calculating the effective memory address and inspecting the source of the value being moved into esi, we can observe that it always takes the second byte of the password hash:

01 0472b2e83c04a8bd2bfe 3cbc1f3d1f0b69df8e93c6542e478601b05d261d 38ceadd5230fc162a56dfae8317a990ad982a88efe9a8392a50e713f
                          |
                          +--> 0xbc is the second byte of the password hash

What follows is a bitwise AND instruction with inputs 0x1f and the value in esi (0xbc in this case).

The bitwise AND operation performs a logical AND on every bit-pair of the two input bytes. If both values of a pair are 1, the result is 1, otherwise 0.

    00011111 <=== 0x1f
AND 10111100 <=== 0xbc
    --------
    00011100 = 0x1c = 28

If 0x1f is fixed, the largest value that can come out of this is 0x1f, or 31, itself.

But what do we do with this value? It turns out that it is used to truncate our XOR “checksum”.

So in our case with the second byte of the password hash being 0xbc, we would have a 0x1c, or 28 byte long checksum at the end:

01 0472b2e83c04a8bd2bfe 3cbc1f3d1f0b69df8e93c6542e478601b05d261d 38ceadd5230fc162a56dfae8317a990ad982a88efe9a8392a50e713f
|  |                    |                                        |
|  |                    |                                        +--> 28 bytes
|  |                    +--> 20 bytes
|  +--> 10 bytes
+--> 1 byte

Now the big question is: Knowing all the components in this 59-byte sequence at path 23.1.5.2.6, can we generate a new salt, compute the derived key/hash, and XOR checksum from a new password of our choice, insert it back into the file, and then open the file using the chosen password?

It could work (based on our assumptions so far). Before we try it out, though, we have to account for one more thing.

If we choose a new password with the same or different salt value, we will most-likely have a different length XOR checksum at the end. This means, we would need to re-align the block (filling it up with NOPs or null-bytes won’t work).

Since this can get complicated, we can use a small trick: we just brute-force a new salt-value which – combined with the password – leads to a 0xbc in the second byte of the SHA-1 hash. This way, the length of the XOR checksum at the end will stay the same and we replace the 59 bytes exactly with another 59-byte long sequence.

So let’s insert the new value, and try to open the file again:

Tamper alert

Oooops! :-) Still not working.

Figuring out the account checksum

Our failure implicitly gave us another hint: there must be another piece of data which also takes the salt and password into consideration – otherwise our little replacement from above would be impossible to be detected as tampering.

So let’s go back to the beginning and have another look at the account section that we parsed out earlier:

(Current path 23.1.5.1)

0x40 (POP)
0x20 (PUSH) 0x2
Path is now 23.1.5.2

0x06 (Key Value) with key 0x04 and length 0x10 (16 bytes)
Path 23.1.5.2.4 ==> 05407cdc76b7f1fd29ac5a9c791af6b8  <=== remember this?

0x06 (Key Value) with key 0x06 and length 0x3b (59 bytes)
Path 23.1.5.2.6 ==> 010472b2e83c04a8bd2bfe3cbc...e9a8392a50e713f

0x06 (Key Value) with key 0x0a and length 0x09 (9 bytes)
Path 23.1.5.2.10 ==> 089fa15b8005967430

0x02 (Key Value) with key 0x0b and a length of 2 bytes
Path 23.1.5.2.11 ==> 0101

0x06 (Key Value) with key 0x10 and length 0x05 (5 bytes)
Path 23.1.5.2.16 ==> 1b3e373334 ===> ("Admin" XORed with 0x5a)

We saw this fixed-size 16-byte long “hash-like” looking sequence of bytes with key 0x04. We previously made the assumption that it could be an MD5 hash (given the length). We also observed that it always completely changes with every change made to the account (changing password, account name, privilege set, etc.).

Hunting for more functions, we eventually see that Draco::DBUserAccount::ComputeCRC is called for every account in the file (you could have also seen that ComputeCRC is on the callstack for some of the other password related functions; info stack).

So if we break at the n-th call to the function, where n is the position of the account, we can continue our investigation.

Getting a first overview of the assembly instructions, it stands out that we have a lot of calls to another function, Draco::CRCContext::Update, which in turn calls OpenSSL’s MD5_Update function.

Debugging functions for which we have documentation and code is always easier. So why don’t we break at every call to MD5_Update until we have a MD5_Final call which finalizes the checksum?

The strategy is the same as before: pause the program when the function is called, then look at the passed values. For OpenSSL’s MD5_Update function we even know the signature, which makes things easier: int MD5_Update(MD5_CTX *c, const void *data, unsigned long len);.

So what’s in the registers when the function is called?

(gdb) info reg
rax            0x7fffffffa880      140737488332928
rbx            0x7fffffffa890      140737488332944
rcx            0x1                 1
rdx            0x10                16
rsi            0x7fffffffa880      140737488332928
rdi            0x60a37dd0          1621327312
rbp            0x0                 0x0
rsp            0x7fffffffa868      0x7fffffffa868
r8             0x0                 0

rdi has the MD5 context, which we can ignore for now. rsi contains a pointer to the data to be included in the hash, and rdx contains its length.

(gdb) x/16xb $rsi
0x7fffffffa880: 0x44    0x8f    0x00    0x0b    0x21    0xe9    0x41    0x2b
0x7fffffffa888: 0xa5    0x9c    0x8c    0x5f    0xd9    0x68    0x13    0xdb

While we don’t know what this sequence of bytes represents, we can just note it down and continue to the next call until the MD5 hash is finalized.

Eventually, we have all inputs to the MD5 hash and can also re-create it in a program of our own. It turns out, when computed again, the hash exactly matches the value stored at 23.1.5.2.4.

But how would we re-compute this without seeing the values from the debugger? For most values that are an input to the hash function, this is relatively easy: you can search for the value in the fmp12 file and note down its path (given it has an adequate length to be unique-ish in the file).

To find the value for a different file, you could just look up the value at the same path again. And if all fails, you could of course also run the debugger again to get to these values.

Do we have it now?

Since we can now freely re-compute the values at 23.1.5.2.4 and 23.1.5.2.6, is it enough to replace the two byte-sequences in a file to open it with a new password?

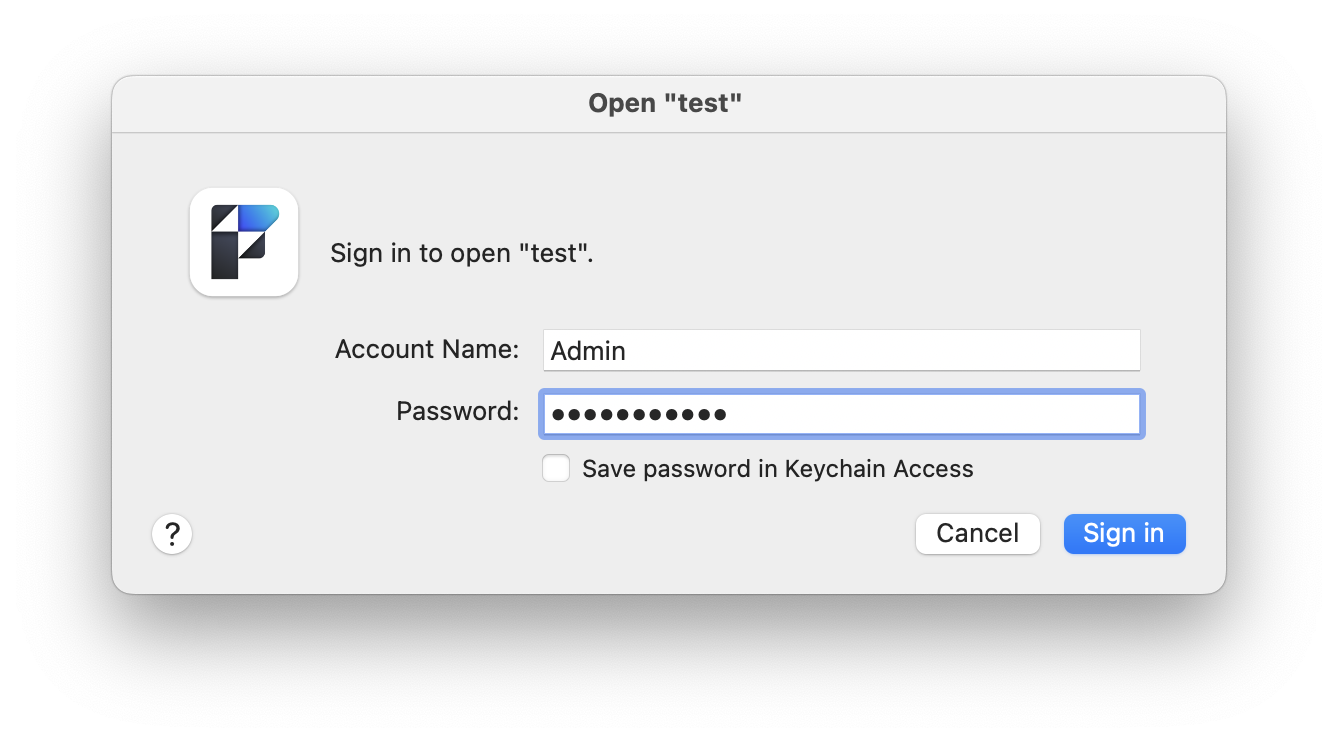
FileMaker login

We enter our new password, and voilà: we’re in :-)

Additional info and caveats

A few important things to note and to answer some questions that came up during my talk:

FileMaker’s Encryption at Rest feature protects you exactly from this (as long as you keep your passphrase secret)
There are and will always be undocumented byte-codes as the specification is not open. In this case you either need to figure out what the byte-code does or you can decide to skip the rest of the payload and jump to the next block. If you are only interested in the account/password information, this is usually not a problem as long as the unknown code(s) don’t appear in exactly the block containing the account information.
Some components that go into the MD5 hash are semantically unclear (to me). In most cases you can just copy the value from the file (if at a known path). If this doesn’t work, you can always get them via the debugger.
If all [Full Access] accounts / the privilege set have been removed from the file and you want to add back such an account, you will need to figure out a lot more than described above. While theoretically possible, it’s probably hard work (need to add back the privilege set, a new account, re-align the blocks, etc.).
Note that you don’t need an account/password if you just want to get a specific piece of data from a file. You can just parse the file as described above and get/export it this way.
Is the file integrity still intact after replacing the hashes? From what I can tell, yes. You can also run a recovery on the file afterwards and it doesn’t flag the changed block as “bad”. However, there’s obviously no guarantee as there’s no official documentation. Changing a password the “normal” way does a bit more to the file, but I don’t think the other changes are particularly relevant (more like modification counts, etc.).
What do the commercial password reset tools do? I don’t have any of those tools, but someone provided me with two fmp12 files; one original and one created using the “Passware” recovery tool. The only difference between the provided files was in the two mentioned paths. So they do exactly the same thing as described in this post.
Is this a vulnerability in FileMaker? No, I don’t consider the possibility of resetting a password in a local unencrypted file to be a vulnerability, so nothing was reported.

Like to comment? Feel free to send me an email or reach out on Twitter.

Was this or any other article on this blog useful to you? If you like and can afford it, you can express your support via this payment link (any amount).

Hi, I'm David