The basics of Logarithms – with examples

Logarithms are widely used in computer science (e.g. for algorithm analyses, floating point number limitations, scaling data, feature transformations). Not coming from a mathematics background (I don’t!) logarithms can seem confusing at first.

Let’s look at the very basics of logarithms to get an understanding of how they can be broken apart, some of the properties that can be utilized, and why they work.

What is a Logarithm?

The logarithm is defined as the inverse operation to exponentiation. To get the logarithm of a number, we need to find out, to what exponent another number, called the base, needs to be raised to produce that first number.

Let’s look at an example:

To rephrase the last sentence again: To get the logarithm of a number 100, we need to find out, to what exponent another number, 10, called the base, needs to be raised to produce that first number 100.

Since \(10^2 = 100\), the logarithm of 100, base 10, is 2:

In Python we would write this as:

>>> math.log10(100)
2.0
>>> 10**2 # "reverse" the operation
100

And to bring it into a general form:

Note that \(\log_{b} x\) only returns real numbers for x >0 (as we will also see on the graph further down).

Now let’s come back to the first sentence of this section: The logarithm is the inverse operation to exponentiation. In other words, it undoes the exponentiation operation.

We can write some code to see this with sample numbers (math.exp(x) returns e to the power of x, math.log(x) returns the logarithm of x in base e).

>>> x = 2.0
>>> math.log(x), math.log(math.exp(x))
(0.6931471805599453, 2.0)
# ==> log(exp(x)) = x

When we plot the two functions, we can see that \(\log (x)\) (i.e. \(\log_{e}x\)) is reflecting \(exp(x)\) (i.e. \(e^x\)).

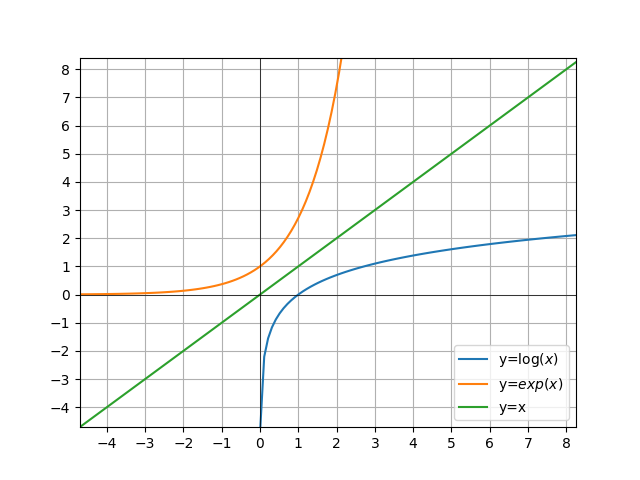
The base

You will most often see logarithms with base e, base 10 or base 2, but the base can be any positive number not equal to 1.

In Python, the most common log bases are available as a function of the math module:

>>> math.log10(100) # base 10
2.0
>>> math.log(100) # base e, or natural log, or ln
4.605170185988092
>>> math.log2(100) # base 2
6.643856189774724
>>> math.log(100, 5) # base 5, or any desired base as second argument
2.8613531161467867

One important property is, that the logarithm of 1 is zero for any base. We can understand this by taking a log apart like in the first section:

10 raised to what power is 1? Only \(10^0\) will equal 1, and the same is true for any other base number. If we plot the ln (log e), log10 and log2, it becomes more clear: for all bases, y is 0 where x is 1.

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0.001, 16, 2000)
y_e = np.log(x)
y_10 = np.log10(x)
y_2 = np.log2(x)

plt.plot(x, y_e)
plt.plot(x, y_10)
plt.plot(x, y_2)

plt.legend(['ln', 'log10', 'log2'], loc='lower right')
plt.xticks(range(math.floor(min(x)), math.ceil(max(x))+1))
plt.axhline(0, color='black', linewidth='0.5')
plt.axvline(0, color='black', linewidth='0.5')

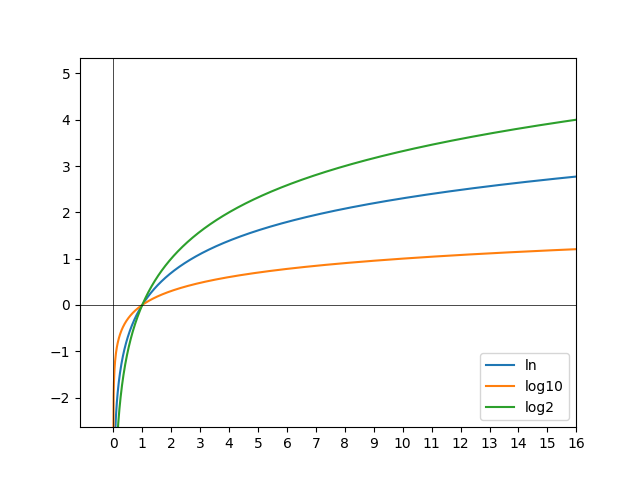
Another visible attribute is that when base and argument are the same number, the result is always 1. Here is the same graph zoomed in a little bit and with grid lines. You can see that for log2 at x = 2, y equals 1, and for the natural log with base e (~ 2.7) and x at e, y also equals 1.

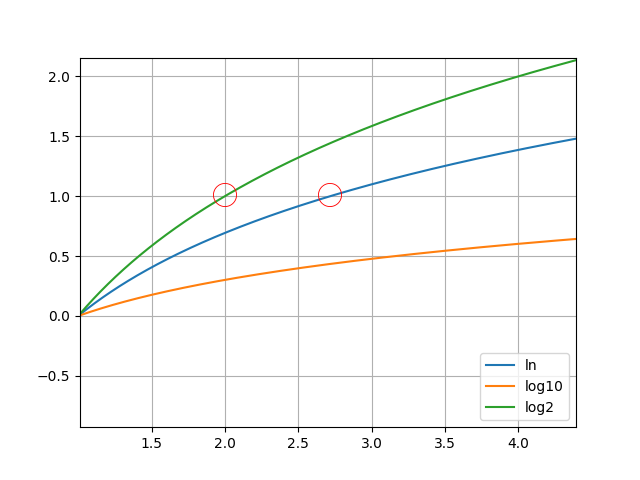
Going to the left side on the x axis, log(x) becomes negative for x < 1 for any base, and diverges towards negative infinity as x approaches zero. The formal way of writing this is:

In the other direction, as x approaches infinity, log(x) diverges towards positive infinity for any base:

Note: When log is written without a base, it usually refers to \(\log_{2}(x)\) in computer science algorithms. In programming/mathematics/machine learning it generally refers to the natural logarithm (e.g. Python math.log or numpy.log), i.e. base e. Base 10 is also commonly implied when you just have \(\log (x)\). 🤔 This is kind of confusing and often just depends on the context. See Wikipedia for more info on particular bases.

Logarithmic rules

Logarithms have important properties, or laws, that one should be familiar with and make computations easier. Let’s have a look at three of them and also understand why they work:

Product rule

The logarithm of a product (multiplication of x and y), can be broken apart and rewritten as the sum of the logarithm of x and the logarithm of y (addition). To see why this formula works, we need to know a property of exponents. Let’s take a look at an example:

We can substitute 8 and 16 as powers of the base, 2.

Using a property of exponents, that says \(a^m \cdot a^n = a^{m+n}\), we can rewrite this as:

Now we need to find the power to which we need to raise 2, the base, to get \(2^{3+4}\). This is obviously 3 + 4 itself. So let’s write this down:

Turning this back into logarithmic form, we get:

Power rule 🚀

With that name it better be good 🤓. And it is. When we have the log of a number raised to a power (here: \(x^y\)), we can bring the exponent down and in front of the log. So for the above equation, it means that the logarithm of x raised to the power of y is equal to y times the logarithm of x. Let’s see why this works by looking at an example:

Another way of looking at this problem is:

From above (product rule) we know that we can turn multiplication into addition. So let’s do that:

And this in turn can be simplified to:

Quotient Rule

Just like with the multiplication to addition (product rule), we can turn devision into subtraction.

We will make up an example and see why this works:

We know that \(\frac{5}{10}\) is the same as \(5 \cdot \frac{1}{10}\) is the same as \(5 \cdot 10^{-1}\). So let’s write out the log again:

Using the product rule (see above), we can turn this into:

And now, using the power rule, we move the -1 down and in front:

So we get:

Change of base

In Python we can calculate the log in any base with math.log(x, base). When you don’t have that function available (like on a calculator), you might want to know how you can easily change the base to a supported one.

The general rule is:

But let’s look at an example again (from base 2 to base 10) and see why this works.

For this equation we know that \(2^x = 16\).

We will now take the log in our desired base 10 on both sides, to be able to use the power rule.

With the power rule we can bring the exponent down and to the front:

To get out final result, we devide both sides by \(\log_{10}(2)\):

More

Much more to cover, but that’s it for now at this point. Take a look at the handy cheat sheet of logarithmic identities for a review of the above, plus additional properties.